Solving CSPs
Now that we know how to model a CSP, let's look at how to solve it.
Backtracking Search
Backtracking Search is a general algorithm that can be used to solve any CSP. The idea is to assign values to variables one at a time, and backtrack when we reach a dead end. The mechanism of the backtracking search algorithm is similar to depth-first search (DFS) algorithm. The difference is that backtracking search will backtrack when it reaches a dead end (and we have a way to check that), while DFS will continue to search until it reaches the end.
Let's start by solving the map coloring problem using backtracking search.
Remember, the goal is to color a map in such a way that no two adjacent regions have the same color. Available colors are red, green, and blue. Below is a map of Australia that we will use to illustrate the problem.
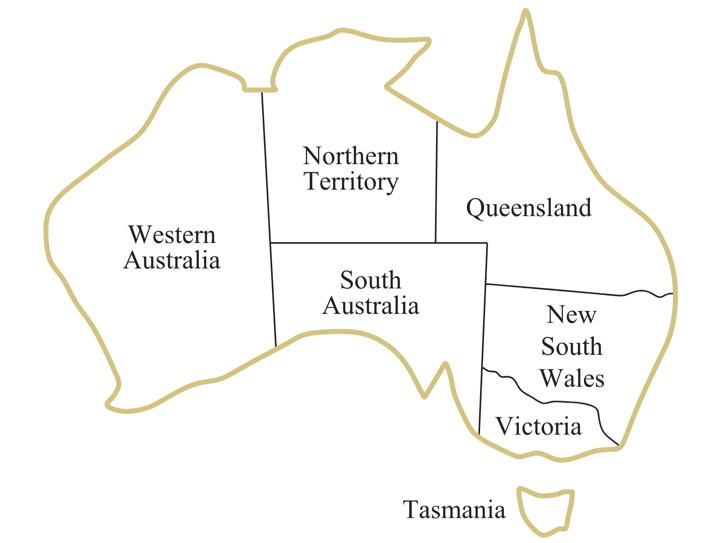
Watch how we solve the problem in the video below:
Notes on the video:
-
The first step is to select an unassigned variable. We started with
WA. We did not consider every possible configuration from that initial empty assignment. We just pickedWAand started exploring the possible values for it.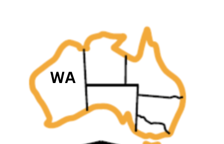
-
From this point, we will explore the possible values for
WAone at a time (red, green, and blue). At this point, we did not check every possible value from the initial assignment.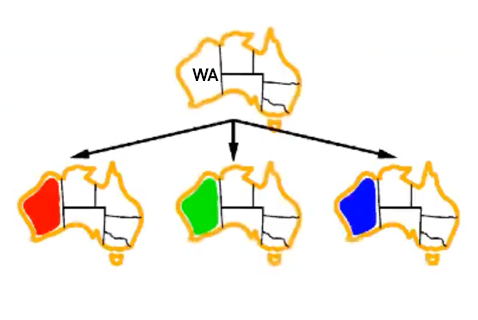
-
From the
WA = redbranch, we will only explore the values for NT that are consistent with the constraints. Some assignments, such as WA = red and NT = red, are not consistent with the constraints, so we will not explore them.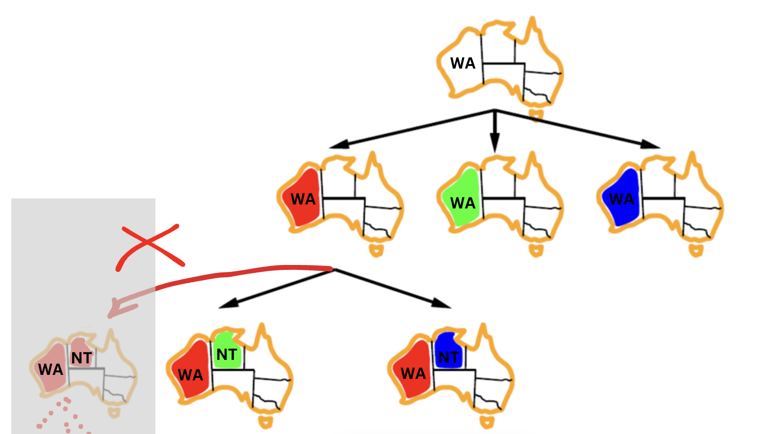
-
Link to the demo tool used in the video: CSP Demo
Let's Code It!

Here is the pseudocode for backtracking search:
![]()
Here is the code in Python:
🎉 Congratulations!🎉
You've just learned a way to solve CSP. You can see that the algorithm has found a solution to the map coloring problem.