Practice Problems

In this lesson, we will solve the 8-puzzle and the 15-puzzle Problem using DFS and BFS.

8-Puzzle Problem

In the 8-puzzle game, we want to find a path from an initial state (scrambled tiles) to the goal state (tiles in the correct order).

Here is a snapshot of our search tree:

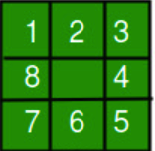
From this state, we can move tiles 2,8,4 and 6. Each of these moves will result in a new state like this:

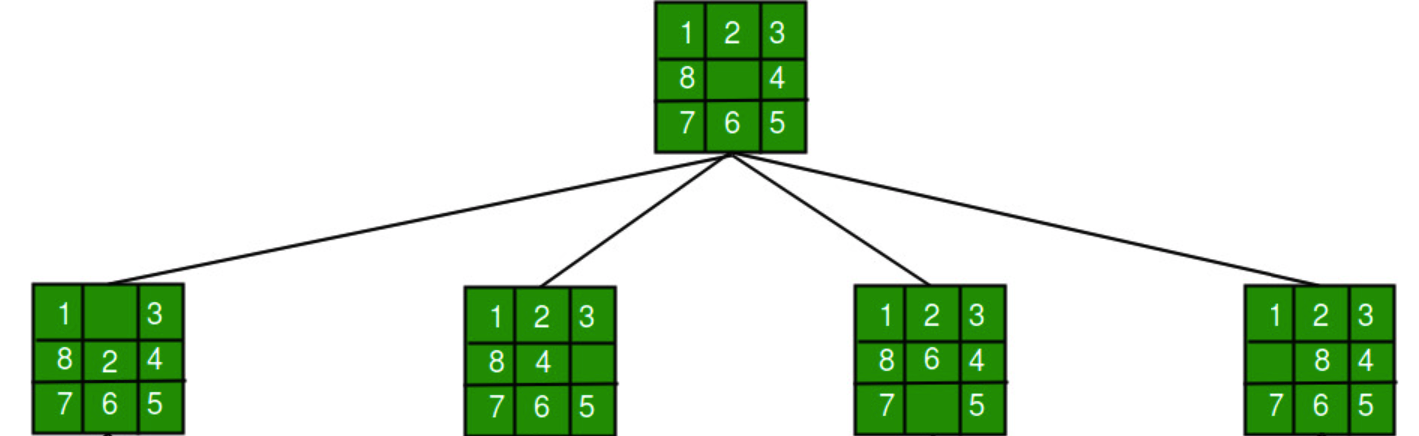
From each new state, we can again move different tiles. Each of these moves will result in a new state until we reach the goal state.

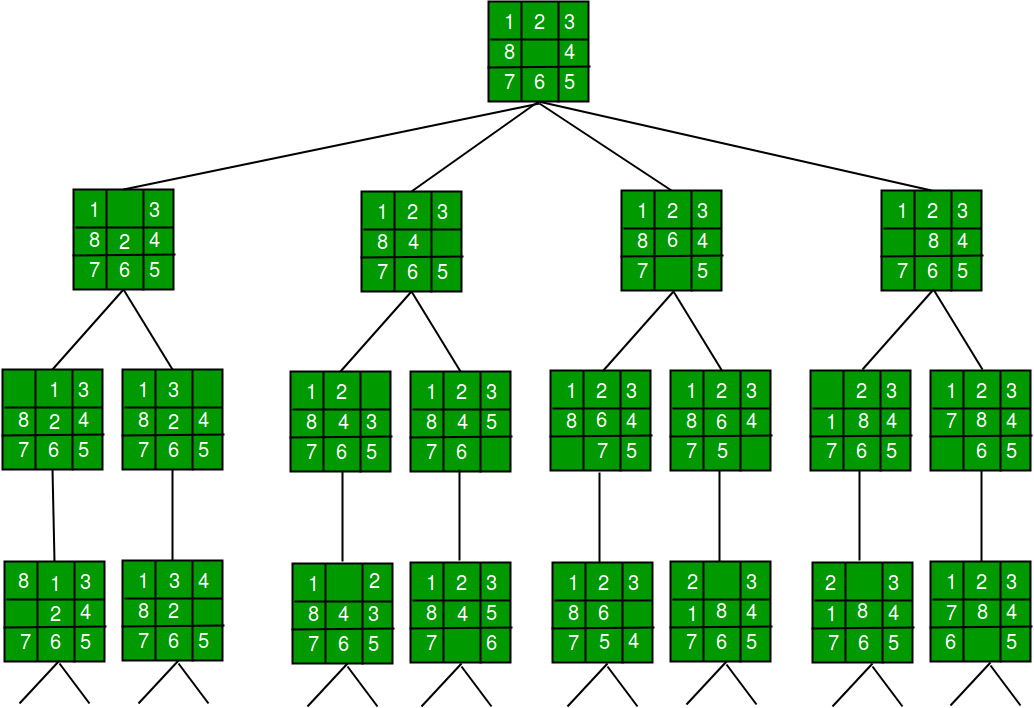
Solving the 8-Puzzle Problem with BFS:

In the code below, we will solve the 8-puzzle problem using the Breadth-First Search (BFS) algorithm.

Try It Yourself First

Before looking at the code, try to solve the problem yourself. This is invaluable for your learning. You can start by answering and coding the following questions:

Environment: What is our environment/world. How to model that in code. How is our initial state and goal state look like? Write the code for that.

Here's an example of how you might start coding:

initial_state = # YOUR CODE HERE
goal_state = # YOUR CODE HERE

Transition Model: What is our transition model. How to move from one state to another. Write the code for that.

Your code could be something like:

  def make_move(current_state, move):
    # YOUR CODE HERE
    return new_state

Goal Test: What is our goal test? How to check if we have reached the goal state? Write the code for that.

Solution: Use BFS to build the search tree and explore the states of the corresponding actions.

timer 30 minutes

Code Walkthrough

Our World (Environment)

Our world consists of a 3x3 grid. We will represent the grid as a 1D array of size 9. The empty tile will be represented by the None value.

  initial_board = [8,3,1,7,2,6,5,4, None]
  goal_board = [1, 2, 3, 4, 5, 6, 7, 8, None]

Our transition model will be moving the empty tile up, down, left, or right. So we have the current state of the board and the move we want to make. The make_move function will return the new state of the board after making the move.

def make_move(board, move):
  empty_pos = board.index(None)

  if not is_valid_move(empty_pos, move):
    return None

  # calculate the row and column (respectively) in the 2-dimensional grid that corresponds to the position empty_pos in the 1-dimensional array representation of the grid. 

  row, col = divmod(empty_pos, N) # what is the row and column indices of the empty tile
  if move == 'up':
    target_pos = (row - 1) * N + col
  elif move == 'down':
    target_pos = (row + 1) * N + col
  elif move == 'left':
    target_pos = row * N + (col - 1)
  else:  # move == 'right':
    target_pos = row * N + (col + 1)

  new_board = board[:]
  new_board[empty_pos], new_board[target_pos] = new_board[
      target_pos], new_board[empty_pos]
  return new_board

Goal Test

Our goal test will be to check if the current state of the board is equal to the goal state.

   if board == goal_board:
      return path

BFS Algorithm

def bfs(initial_board, goal_board):
  visited = set()
  queue = deque([(initial_board, [])])

  while queue:
    board, path = queue.popleft()

    if board == goal_board:
      return path

    visited.add(tuple(board))

    for move in ['up', 'down', 'left', 'right']:
      next_board = make_move(board, move)
      if next_board and tuple(next_board) not in visited:
        queue.append((next_board, path + [move]))

  return None

The complete code in Replit can be found and tested below:

Play it!

Test the algorithm's correctness by playing the game online using the generated result from the algorithm. An online game can be found here.

[Task] Solve it using DFS

15-Puzzle Problem

The 15-puzzle is the same as the 8-puzzle but with 15 tiles instead of 8. The tiles are numbered from 1 to 15. The goal state is to arrange the tiles in ascending order from left to right and top to bottom, with the empty space in the bottom right corner.

Solving the 15-puzzle Problem using BFS

The code is exactly the same as the 8-puzzle problem but with a few modifications to the board dimension and the goal board.

🛑 Critical Warning: Diving into Complexity

I've included a straightforward and solvable configuration in the code above for us to test. However, numerous other configurations will take an extensive amount of time to solve. Your computer's memory will mostly run out, and the program will crash before completing the solution.

Additionally, some configurations are unsolvable. You can find solvable configurations on online games, such as this one.

🙎🏽 Failure of BFS and DFS

The 15-puzzle problem is way more complex than the 8-puzzle problem. The 8-puzzle problem has 9! = 362,880 states, while the 15-puzzle problem has 16! = 20,922,789,888,000 states. This is a huge number of states to explore. Even with the BFS algorithm, it will take a long time to find the solution. With DFS, it will take even longer. It will take so long that it will be impractical to use any of them to solve the 15-puzzle problem.

That's why we need to use more efficient algorithms to tackle this complexity. In the next lesson, we will learn about informed search algorithms and how to use them to efficiently solve this problem.

Artificial Intelligence

Test the algorithm's correctness by playing the game online using the generated result from the algorithm. An online game can be found here.