Search Problem Modeling
Ready for some excitement?
Would you be interested in learning how to program a computer to solve mazes, puzzles, find paths, or optimize item arrangements? What if you could also use this knowledge to minimize your time spent in traffic or create a system that plays chess or solves a Rubik's cube? This is precisely the essence of our lesson on "Search."

Search Problems
A search problem is a specific type of computational problem that involves exploring a set of possible states or configurations (known as the state space) and finding a sequence of actions to achieve a goal within this state space.
This is a broad definition, so let's clarify it with an example.
Consider the scenario of a car moving from point A to point B, as illustrated below:

To reach point B, the car can follow various paths, as shown in the image below:
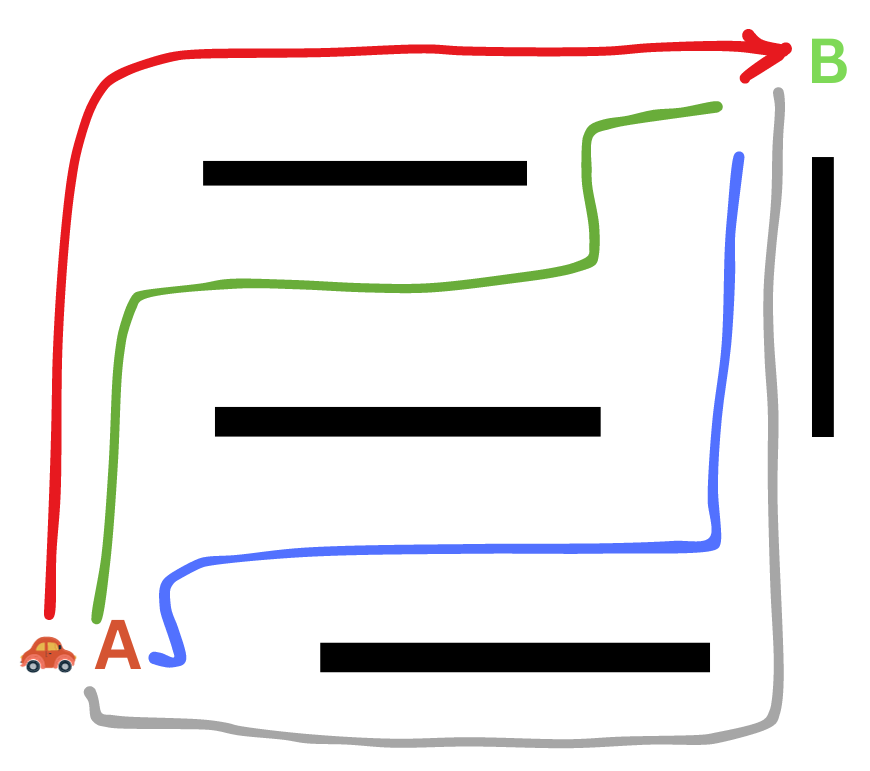
This is a search problem identified by the following:
- We have an agent (the car) that is trying to find a solution (the path) within a defined problem space (the road).
- The agent in this case is called a problem-solving agent.
- The problem space, or state space, consists of various states or configurations (the different positions of the car).
- The goal is to find a sequence of actions that will lead from an initial state (the starting position of the car) to a desired goal state (the destination).
The 8 Queens Problem
Let's consider another example. If we have a chessboard and eight queens, how can we place the queens on the chessboard so that no queen can attack another queen? This is known as the 8 queens problem.
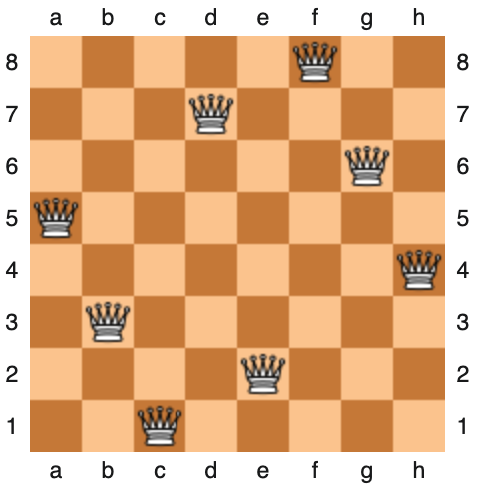
This is also a search problem identified by the following:
- There are various configurations (states) of the queens on the chessboard.
- The goal is to find a sequence of actions that will lead from an initial state (empty board) to a desired goal state (the configuration of the queens on the chessboard so that no queen can attack another queen).
More Examples
Here are a few more examples of search problems:
- Finding the optimal path for data packets to travel from a source to a destination
- Solving puzzles like Sudoku or Rubik's Cube
- Determining the optimal route between two locations on a map
You will learn how to solve such problems in this course 🚀.
🎯 Understanding Our Objective
One might question whether we are genuinely searching for something in this context. Well, you can think of the solution itself as the object of our search.
The solution is the sequence of actions that will lead us from the initial state to the goal state.
In the car example, our mission is to discover the path leading us to point B (by searching possible states). In the 8-queens problem, our mission is to find the configuration of the queens on the chessboard (by searching possible states starting with an initial one).
Modeling Search Problems
To tackle these problems with a computer, we aim to create a computer-friendly representation, a computational model. A typical model of a search problem consists of the following:
State Space:
This represents the different configurations of the problem space. For instance, the different positions of the car, the different arrangements of tiles in a puzzle, or the different configurations of a robot.
Initial State:
The starting state of the problem. For example, the starting position of the car, the initial arrangement of tiles in a puzzle, the initial position of a robot, etc.
Goal State:
The desired state of the problem. For example, it could be the car's destination, the desired puzzle tile arrangement, or the robot's target position. A goal test is a function that determines whether a given state is a goal state. For instance, checking if the car has reached its destination, if the puzzle tiles are in the correct order, or if the robot has arrived at its destination.
Actions:
Actions are the possible moves or steps that can transition the system from one state to another. These can include actions like moving up, down, left, or right.
Transition Model:
The transition model (or Successor Function) is a function that accepts a state and an action as input and yields an allowable new state as output. For example, the transition model for the car problem would take the car's current position and the desired direction, Up for example, as input and return the new position as output.
Solution:
The solution is a series of actions that lead from the initial state to the goal state. This could be the path the car takes from its starting point to its destination, the sequence of moves needed to solve the puzzle, or the route the robot follows to reach its goal.
Modeling the Car's Journey
Let's explore our previous example of a car journeying from point A to point B and frame it as a search problem. Our focus in this lesson is on modeling the problem's state space, initial state, goal state, goal test, actions, and transition model. The solution will be discussed in an upcoming lesson.
State Space:
To model the state space, we need to consider all the possible configurations of the car. To do that, we need to decide how we will represent the car's position and the environment in which it is moving.
To simplify things, we can represent the car's position as a coordinate on a grid. For example, the car's position at point A can be represented as (1,0), and its position at point B can be represented as (6,6).
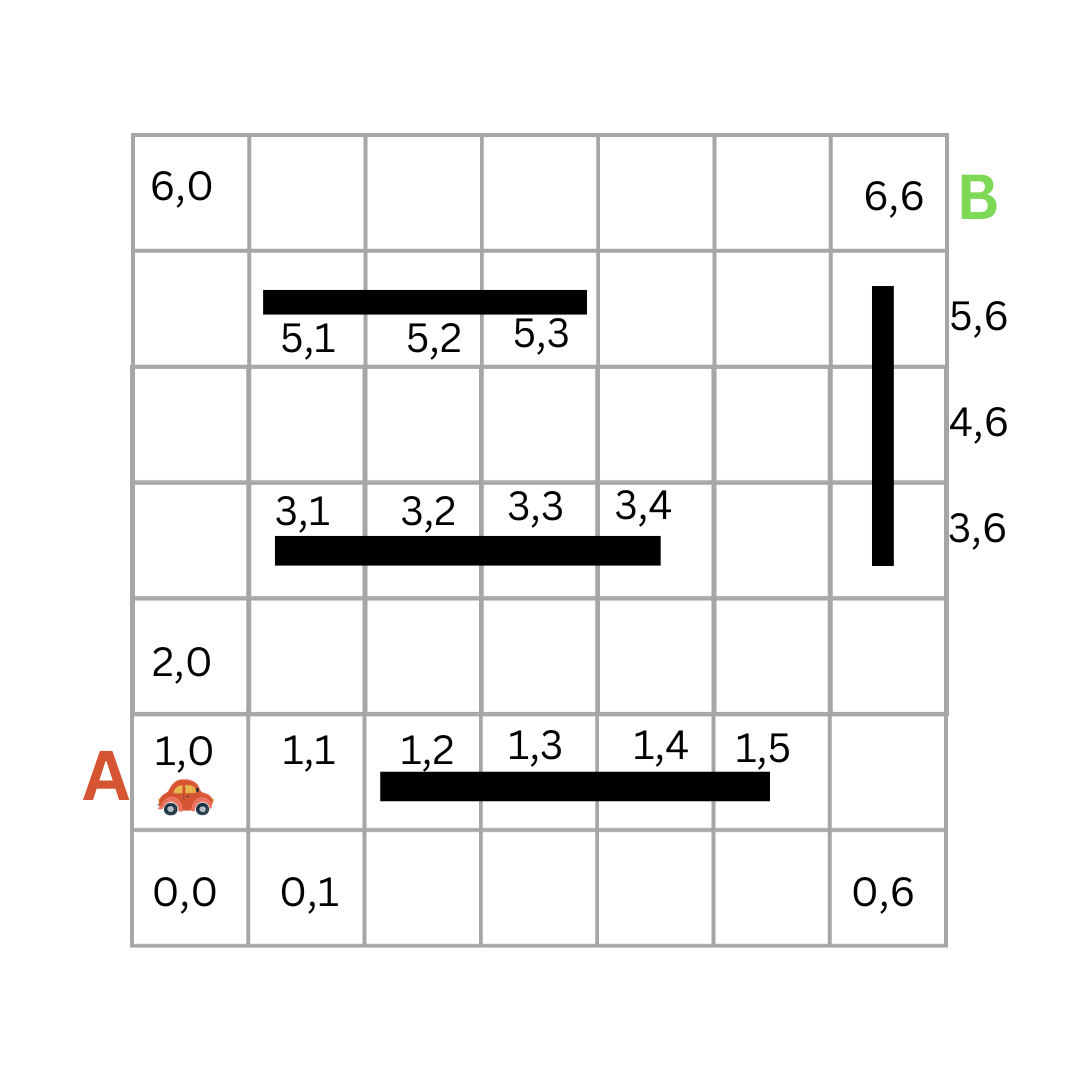
So, the state space is all the possible positions of the car on the grid. This is a finite set of states, and we can represent it as a list in Python.
state_space = []
GRID_SIZE = 6
for i in range(GRID_SIZE):
for j in range(GRID_SIZE):
state_space.append(1)
Important Note: The state space in this example is small enough to be represented as a list. However, in most cases, the state space is too large to be represented as a list, as in this example, and we don't need to store the entire state space upfront. More information on this will be provided later.
Initial State:
After modeling the state space, it is clear now that our initial state is the position of the car at point A, which is (1, 0). We can represent the initial state as a tuple in Python.
initial_state = (1, 0)
Goal State and Goal Test:
The goal state is the position of the car at point B, which is (6, 6). Similarly, We can represent the goal state as a tuple in Python.
goal_state = (6, 6)
The goal test will be a function that checks if the car's current position is the same as the goal position. If so, it returns True; otherwise, it returns False.
def goal_test(state):
return state == goal_state
Actions:
Actions are the possible moves or steps that can transition the system from one state to another. In our example, the car can move up, down, left, or right. We can represent the actions as a list in Python.
actions = ["up", "down", "left", "right"]
Transition Model (Successor Function)
At a specific state, the agent can take one of the possible actions: up, down, left, or right. For each specific action, the agent will end up in a new state.
Try it!
Take 10 minutes and try to write a transition model function for our car example. It's a function that should take a state and an action as input and return a new state as output.
def transition_model(state, action):
# Your code here
Recall that the current state is the position of the car within the grid. The action is the direction the car is moving in. For example, if the car is at position (1, 1) and the action is up, the newly returned position will be (2, 1).

Don't rush through it. This is a crucial step in your learning process. If you can't do it, you can check the solution below. But, please, try to do it first.

Unfold the sample code below for an idea of how a transition model for this environment can be implemented.
Transition Model Function
def transition_model(state, action):
x, y = state
if action == 'up':
return (x, y + 1)
elif action == 'down':
return (x, y - 1)
elif action == 'left':
return (x - 1, y)
elif action == 'right':
return (x + 1, y)
else:
raise ValueError(f"Unknown action: {action}")
- Note: The sample code above does not check if the new state is valid or not.
Exercise: The 8-Puzzle Problem
Now, it's your turn to model a search problem.
The 8-puzzle was invented and popularized by Noyes Palmer Chapman in the 1870s. It is played on a 3-by-3 grid with 8 square blocks labeled 1 through 8 and a blank square. Your goal is to rearrange the blocks so that they are in order. You are permitted to slide blocks horizontally or vertically into the blank square.
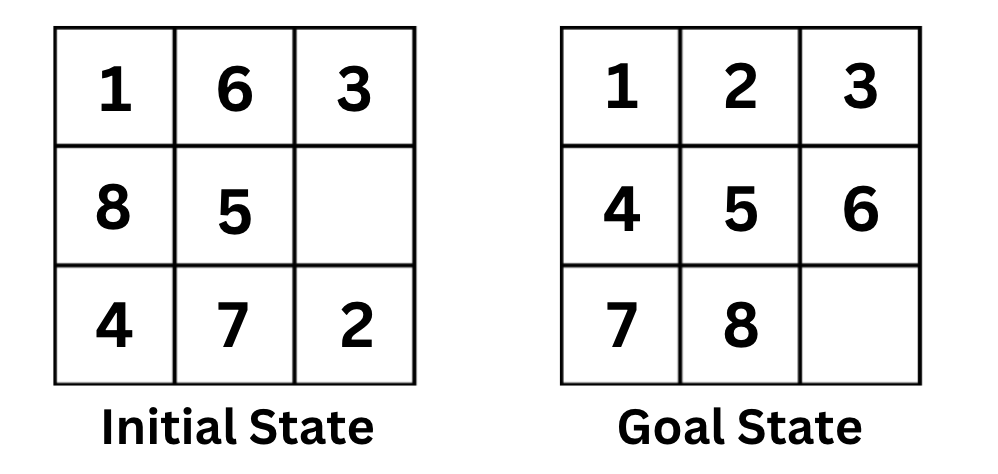
Take 10-15 minutes and try to model this problem. Describe the state space, initial state, goal test, actions, and transition model.
This is a crucial step in your learning process. Don't rush through it.

🧩 Unfold the solution below and match it with your solution.
Solution
State Space: The state space is all the possible configurations of the puzzle tiles. [[1, 3, 2], [6, 4, 7], [7, 8, None]] and [3, 1, 2], [6, 4, 7], [8, 7, None]] are two examples of states in the state space.
Initial State: The initial state is the starting configuration of the puzzle, which may initially be a scrambled arrangement of the tiles. For example, [[1, 3, 2], [6, 4, 7], [7, 8, None]].
Goal State: The goal state is the desired configuration where the tiles are arranged in ascending order [[1, 2, 3], [4, 5, 6], [7, 8, None]]. The Goal Test is a function that checks if the current state is the goal state.
Actions: Moving the blank tile up, down, left, or right.
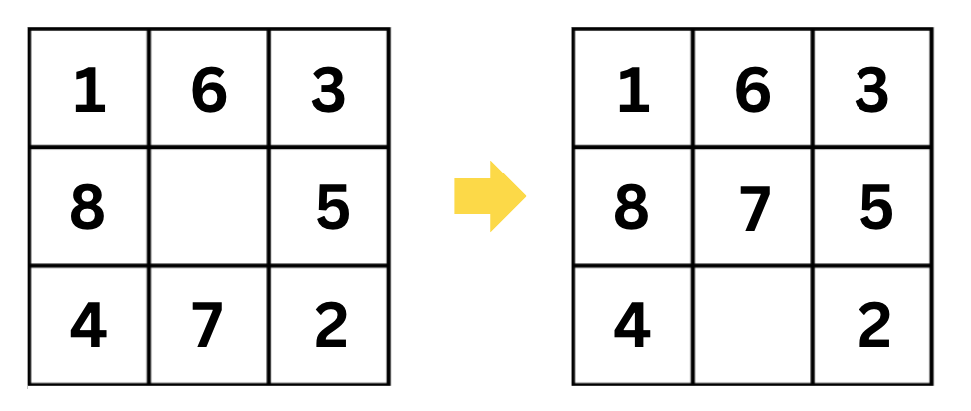
Transition Model: This function defines the outcome of applying an action to a given state, resulting in a new state. For example, if the current state is [[1, 6, 3], [8, None, 5], [4, 7, 2]] and the action is up, the new state will be [[1, 6, 3], [8, 7, 5], [4, None, 2]]
🎉 Congratulations!🎉
You have just completed modeling your first search problem!
State and State Space Representation
In any search problem, the method of representing states and state space significantly influences the efficiency of our search algorithms.
For example, in the car navigation problem, rather than using a tuple representation, we can opt for a graph representation. In this scenario, nodes symbolize specific car configurations, while edges illustrate permissible movements between them.
Likewise, in the 8-puzzle problem, a graph representation is applicable, where each node denotes a specific puzzle configuration, and the edges represent the feasible transitions between configurations.
Choosing a graph representation may provide the flexibility to utilize various graph algorithms, potentially optimizing the search process and improving problem-solving efficiency.
This concept can be expanded further by incorporating additional information into the representation, such as the estimated cost of reaching the goal from a particular state, to guide the search process and enhance the search algorithms' efficiency.
💡 Exploring different methods for representing states and state spaces is an interesting area of research. You could be the next person to devise an innovative representation of states and state spaces for a specific problem, thereby making your mark as a computer scientist in the field.
Can you think of other ways to represent states and state spaces for any of the problems discussed in this lesson?
💬 Discuss and share your thoughts with us here.
Self Assessment!
-
What is a search problem?
-
What are the components of a search problem?
-
Give a complete problem formulation for each of the following problems. Choose a formulation that is precise enough to be implemented.
-
There is an n×n grid of squares, each square initially being either an unpainted floor or a bottomless pit. You start standing on an unpainted floor square and can either paint the square under you or move onto an adjacent unpainted floor square. You want the whole floor painted.
-
Your goal is to navigate a robot out of a maze. The robot starts in the center of the maze facing north. You can turn the robot to face north, east, south, or west. You can direct the robot to move forward a certain distance, although it will stop before hitting a wall.
-
Unfold the sample solutions below to check your answers.
Sample Solutions
1. n×n grid of squares
State space: all possible configurations of the floor tiles and your position.
Initial state: all floor squares unpainted, you start standing on one square unpainted floor square. Actions: paint square, move to adjacent floor square.
Goal test: all floor squares painted.
Successor function: paint current tile, move to adjacent unpainted floor tile.
2. navigate a robot out of a maze
We’ll define the coordinate system so that the center of the maze is at (0, 0), and the maze itself is a square from (−1, −1) to (1, 1).
State space: all possible locations and directions of the robot.
Initial state: robot at coordinate (0, 0), facing North.
Actions: turn north, turn south, turn east, turn west, move forward.
Goal test: either |x| > 1 or |y| > 1 where (x, y) is the current location.
Successor function: move forwards any distance d; change direction robot it facing. Cost function: total distance moved.