Gradient Descent

We have learned about linear regression and how to use it to predict the value of an output variable based on the value of one input variable(feature). We have also learned about the cost function and how to use it to measure the error of the model. In this lesson, we will learn about gradient descent, a popular optimization algorithm used to minimize the cost function.

Watch the following videos in the given order:

Introduction to Gradient Descent:

Gradient Descent Implementation:

Key points from the videos:

Gradient Descent

Gradient descent is an optimization algorithm used to minimize the cost function. The cost function is a function that measures the error of the model. The cost function for linear regression is the mean of squared error.

The equation of the gradient descent algorithm is as follows:

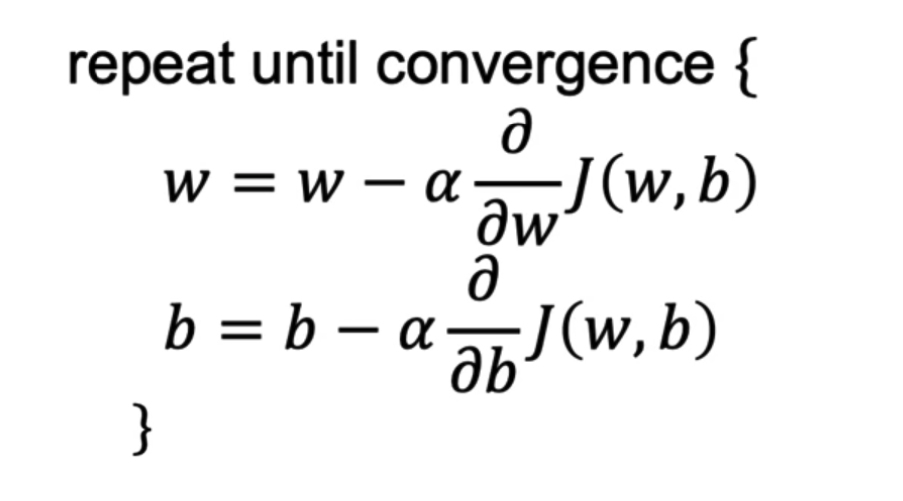
• The idea of gradient descent is to start with a random value for the coefficients and then iteratively update the coefficients in the direction of the gradient of the cost function until we reach a local minimum.

• The derivative term in the gradient descent equation tells us in which direction we should update the coefficients. In combination with the learning rate, the derivative term tells us how much we should update the coefficients.

• If we are already at a local minimum, the derivative term will be zero and the coefficients will not be changed.

The Learning Rate and Number of Iterations:

• The learning rate is a hyperparameter that controls how much we update the coefficients in each iteration.
• The learning rate is usually set to a small positive number between 0 and 1.
• If the learning rate is too small, the algorithm will take a long time to converge. If the learning rate is too large, the algorithm may overshoot the minimum and potentially never converge.
• The number of iterations is another hyperparameter that controls the number of iterations the algorithm will run. If the number of iterations is too small, the algorithm may not converge. If the number of iterations is too large, the algorithm will take a long time to converge.

Gradient Descent for Linear Regression:

Practice Quiz:

Q. Which of the following are true statements? Select all that apply.

1. To make gradient descent converge, we must slowly decrease alpha (α) over time.

2. Gradient descent is guaranteed to find the global minimum for any function J(θ0, θ1).

3. Gradient descent can converge even if α is kept fixed. (But α cannot be too large, or else it may fail to converge.)

4. For the specific choice of cost function J(θ0, θ1) used in linear regression, there are no local optima other than the global optimum.