Informed Search
In our previous lessons, we learned about the breadth-first search and depth-first search algorithms. Both of these algorithms do not use any additional information to guide their search. These algorithms are called uninformed search algorithms.
Uninformed search algorithms typically explore all possible states within the search space systematically. They do so without any additional knowledge or heuristics guiding their search, hence the term "uninformed."
In this lesson and the following one, we will learn about the greedy best-first and the A* search algorithms, which are informed search algorithms.
Informed search algorithms use additional information or heuristics to guide the search towards promising areas of the search space. These algorithms aim to find an optimal or close-to-optimal solution more efficiently by prioritizing the exploration of states that are likely to lead to the goal state. As a result, informed search algorithms often do not need to explore all possible states to find a solution, especially if the heuristic is well-designed and provides accurate estimates of the remaining cost to the goal.
ristic is well-designed and provides accurate estimates of the remaining cost to the goal.
Informed Search
To get a sense of how informed search algorithms work, let's consider our car example. Take a look at this image:
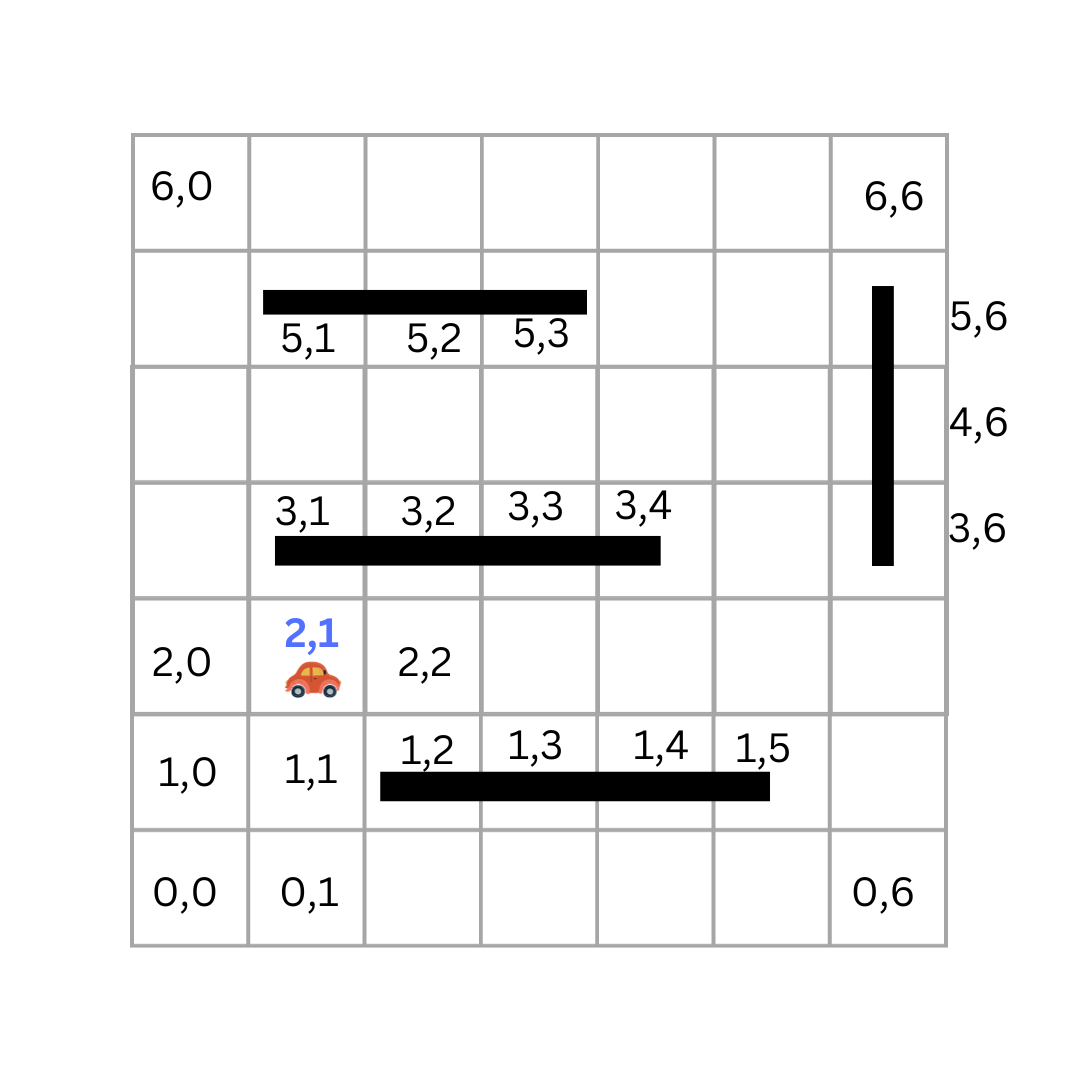
If the car is at position (2,1) , as humans, we can easily determine that the next step should be to move to (2,2). The (1,1) cell will take us further away from the goal state. This is an example of an informed decision. We use our knowledge of the problem to make a better decision.
Greedy best-first search
Greedy best-first search is an informed search algorithm that uses a heuristic function to guide its search.
A heuristic function is a function that assesses alternatives in search algorithms at each branching step, utilizing available information to determine which branch to follow (which next state to explore).
In our previous car example, if we can inform the algorithm to prioritize the point (2,2) as it is closer to the goal state than (1,1) , then the algorithm will be able to make a better decision. In a grid world, we can use the direct line distance between the goal state and each state as a heuristic function.
A good heuristic function for the 15-Puzzle problem could be the number of misplaced tiles. The number of misplaced tiles is the number of tiles that are not in their correct position. To implement this heuristic function, we can simply compare the current state with the goal state and count the number of misplaced tiles.
def count_misplaced_tiles(board, goal_board):
out_of_place_tiles_count = 0
for i in range(N * N):
if board[i] != goal_board[i]:
out_of_place_tiles_count += 1
return out_of_place_tiles_count
Let's solve the 15-Puzzle problem using the greedy best-first search algorithm and see how it performs.
Solving the 15-Puzzle Problem with Greedy Best-First Search
The output of the program is:
Greedy BFS Solution:
# some steps omitted
......
Move left:
[1, 2, 0, 7]
[5, 6, 4, 3]
[9, 10, 11, 8]
[13, 14, 15, 12]
Move left:
[1, 2, 0, 4]
[5, 6, 3, 7]
[9, 10, 11, 8]
[13, 14, 15, 12]
Move down:
[1, 2, 3, 4]
[5, 6, 0, 7]
[9, 10, 11, 8]
[13, 14, 15, 12]
Move right:
[1, 2, 3, 4]
[5, 6, 7, 0]
[9, 10, 11, 8]
[13, 14, 15, 12]
Move down:
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 11, 0]
[13, 14, 15, 12]
Move down:
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 11, 12]
[13, 14, 15, 0]
178
My computer was able to show me the solution of the 15-Puzzle problem in less than a second. This is a huge improvement over the BFS algorithm. The BFS algorithm took a long time to find the solution and most of the time it ran out of memory.
Different Heuristic Functions
Depending on the specific characteristics of the problem at hand, various heuristic functions can be designed to guide the search algorithm effectively. In our car example, the direct line distance, known as Euclidean distance, between the goal state and each state serves as one heuristic function. Manhattan distance, which is the distance between two points measured along axes at right angles, serves as another one. In maze-solving problems, a heuristic could involve estimating the remaining steps to the goal based on the current position.
Summary
In conclusion, the transition from blind search algorithms, such as breadth-first search and depth-first search, to informed search algorithms marks a significant leap in computational efficiency. The drawbacks of uninformed searches, as exemplified by the 15-puzzle problem, underscore the need for additional information to guide the search process effectively.
In this lesson, we delved into the greedy best-first algorithm, which leverages heuristic functions to make informed decisions during exploration. The practical application of this algorithm in solving the 15-Puzzle problem showcased its ability to find solutions more efficiently, addressing the limitations of uninformed searches.
As we progress, exploring various heuristic functions in upcoming lessons, we continue to uncover their diverse applications and refine our understanding of their impact on algorithmic performance.